Tổng hợp công thức tính đạo hàm theo Tài liệu của Bộ trưởng Bộ GDĐT

Tổng hợp công thức tính đạo hàm (Hình từ Internet)

Tổng hợp công thức tính đạo hàm theo Tài liệu của Bộ trưởng Bộ Giáo dục và Đào Tạo

Tại Quyết định 2370/QĐ-BGDĐT năm 2024, Bộ trưởng Bộ Giáo dục và Đào tạo ban hành Tài liệu hướng dẫn dạy học môn Toán lớp 11. Theo đó, tổng hợp công thức tính đạo hàm như sau:

Công thức tính đạo hàm của hàm số y=xⁿ, n∈ℕ* như sau:

Hàm số y=xⁿ n∈N* có đạo hàm trên R và (xⁿ)’=nx^n-1.

VD: y=x⁷ có đạo hàm y’=7x⁶

Công thức tính đạo hàm của hàm số y=√x như sau:

Công thức tính đạo hàm của hàm số lượng giác:

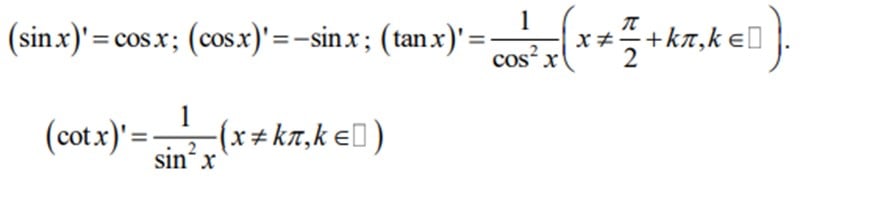
Công thức tính đạo hàm của hàm số mũ và hàm số logarit:

Công thức tính đạo hàm của tổng, hiệu, tích, thương của hai hàm số:

Công thức tính đạo hàm hợp: y_x’=y_u’.u_x’

Mục tiêu và những điều cần lưu ý khi dạy học các công thức tính đạo hàm

Theo Tài liệu tại Quyết định 2370/QĐ-BGDĐT năm 2024, mục tiêu và những điều cần lưu ý khi dạy học các công thức tính đạo hàm như sau:

(1) Mục tiêu

(i) Năng lực

- Tính được đạo hàm của một số hàm số sơ cấp cơ bản.

- Sử dụng được các công thức tính đạo hàm của tổng, hiệu, tích, thương của các hàm số và đạo hàm của hàm hợp.

- Mô tả được một số vấn đề có liên quan đến môn học khác hoặc có liên quan đến thực tiễn gắn với đạo hàm.

(ii) Phẩm chất

- Ham học hỏi, có ý thức tìm tòi, khám phá tìm hiểu về các quy tắc tính đạo hàm.

- Có ý thức làm việc nhóm; sẵn sàng chịu trách nhiệm với lời nói và việc làm của bản thân; hoàn thành các nhiệm vụ học tập của chủ đề các quy tắc tính đạo hàm.

(2) Những điều cần lưu ý

** Lưu ý dạy học

- Bài học này cung cấp các quy tắc tính đạo hàm của tổng, hiệu, tích, thương các hàm số, đạo hàm của hàm số hợp và công thức đạo hàm của những hàm số sơ cấp cơ bản. Sau bài học này, về nguyên tắc HV có thể tính được đạo hàm của các hàm số sơ cấp thường gặp. Một điểm khác biệt so với SGK Toán lớp 11 trước đây là ở đây trình bày cả các công thức tính

đạo hàm của hàm số mũ và hàm số lôgarit, vì trong Chương trình mới hai loại hàm số này đã được giới thiệu ở lớp 11.

- Một trong những kĩ năng quan trọng nhất của bài này là cách tính đạo hàm của hàm số hợp. Đây là kĩ năng cực kì thiết yếu mà HV cần nắm vững.

- Do tinh thần giảm tính hàn lâm của Chương trình mới, nền SGK Toán 11 không trình bày khái niệm hàm số luỹ thừa với số mũ thực tổng quát và công thức tính đạo hàm của nó như ở SGK Toán THPT trước đây, mà chỉ trình bày công thức tính đạo hàm của hàm số y = xⁿ với số mũ n nguyên dương và công thức tính đạo hàm của hàm số y =√x

- GV cần khai thác các cơ hội để có thể hình thành và phát triển các năng lực Toán học cho HV, tùy theo thời điểm cụ thể trong bài phù hợp với đặc trưng của năng lực đó. Chẳng hạn HV có cơ hội phát triển:

+ Năng lực tư duy và lập luận toán học: Thông qua các thao tác nhận ra sự tương đồng và khác biệt về số mũ khi HV thực hiện việc khái quát đạo hàm của nx từ kết quả của đạo hàm x², nhận biết sự tương đồng giữa 10^x và a^x để tính đạo hàm của hàm số y=a^x ,…

+ Năng lực giải quyết vấn đề toán học: Thông qua các thao tác xác định được cách thức để thực hiện các ví dụ, bài tập.

+ Năng lực mô hình hoá toán học: Thông qua các thao tác sử dụng đạo hàm để tìm thời điểm mà tốc độ của viên đạn bằng 0,…

Trên đây là nội dung tổng hợp công thức tính đạo hàm theo Tài liệu tại Quyết định 2370/QĐ-BGDĐT năm 2024.

Lê Quang Nhật Minh